Various vector calculus interacts to play with.

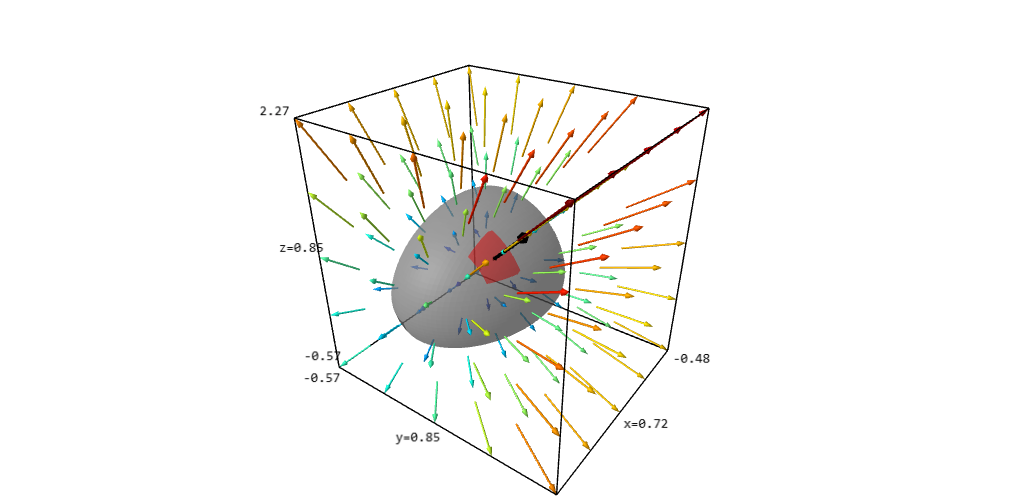
In the interact below, $g$ is a scalar function of three variables $x,y,z$, $P$ is a point at which to evaluate $g$, the grey surface is the level surface $g(x,y,z)=g(P)$. The arrows show the gradient vector field of $g$. The $lc$ and $uc$ boxes allow you change the lower corner and upper corner of the viewing box. The $k$ box controls the number of arrows showing the gradient vector field of $g$.

In this interact, you choose a vector field $G$ and a viewing box with lower corner $lc$ and upper corner $uc$. The red arrows show the vector field $G$. The black arrows show the curl of $G$.

Here you choose a field $F$, a curve $r$ and its parameter interval $trange$, and the number $pts$ of field and velocity vectors to show along the curve. You get a picture and the value of the line integral of $F$ along the curve.

This interact computes the surface area of the graph of the function $f$ over the rectangle given by $urange \times vrange$.