Gradient, Divergence, and Curl
Various vector calculus interacts to play with.
Push the Start button before starting any interact
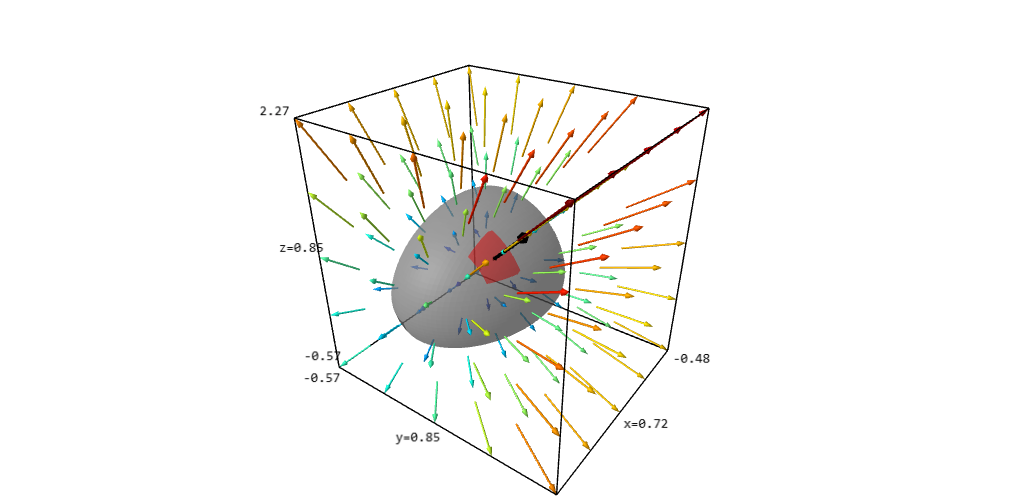
Scalar functions, their level surfaces and gradient fields
In the interact below, $g$ is a scalar function of three variables $x,y,z$, $P$ is a point at which to evaluate $g$, the grey surface is the level surface $g(x,y,z)=g(P)$. The arrows show the gradient vector field of $g$. The $lc$ and $uc$ boxes allow you change the lower corner and upper corner of the viewing box. The $k$ box controls the number of arrows showing the gradient vector field of $g$.
Vector fields and their curls.
In this interact, you choose a vector field $G$ and a viewing box with lower corner $lc$ and upper corner $uc$. The red arrows show the vector field $G$. The black arrows show the curl of $G$.
Line integral of the tangential component of a vector field along a curve
Here you choose a field $F$, a curve $r$ and its parameter interval $trange$, and the number $pts$ of field and velocity vectors to show along the curve. You get a picture and the value of the line integral of $F$ along the curve.
Length of a curve, mass of a wire.
Here you choose a curve $C$ parameterized by $r(t)=[x(t),y(t),z(t)]$ and its parameter interval $trange=[a,b]$ and a scalar function $f$ defined on $C$. Then $f\circ r$ is defined on $trange$. For example, $f(P)$ might be the density of $C$ at $P \in C$. So $\oint_C f\, ds= \int_a^b f(r(t))\,||dr|| dt$ represents the mass of $C$. Or if $f=1$, then the integral gives the length of $C$. You also get a picture of $C$.
Length, average density, mass and center of mass of a wire.
Here you choose a wire $C$ parameterized by $r(t)=[x(t),y(t),z(t)]$ and its parameter interval $trange=[a,b]$ and a density function $f$ defined on $C$. Then $f\circ r$ is defined on $trange$. So $M=\oint_C f\, ds= \int_a^b f(r(t))\,||dr|| dt$ is the mass of $C$, and the center of mass of the wire is $(M_x/M,M_y/M,M_z/M)$ where $M_x = \oint_C x\,f\,ds = \int_a^b x(t)f(r(t))\,||dr|| dt$ is the moment of the wire about the $x$-axis and similarly for $M_y,M_z$. You also get a picture.
Area of a surface, mass of a plate.
Suppose a surface $S$ in 3-space is parameterized by a function $p(s,t)=(x(s,t),y(s,t),z(s,t))$ defined on a rectangle $R=srange \times trange$, and $g$ is a function defined on $S$. So $g\circ p$ is defined on $R$ and might represent say the density of $S$ at $p(x,y)\in S$ for $(x,y)\in R$. Then the mass of $S$ would be $\iint_S g \, dA = \iint_R g(p(s,t)) ||p_s \times p_t|| \,ds\,dt$. In particular, if $g = 1$, then the integral would be the area of $S$. This interact computes $\iint_S\, g \, dA = \iint_R \, g(p(s,t))\, ||p_s\, \times\, p_t|| ds\, dt$.
Area of a surface, mass, average density and center of mass of a plate.
Suppose a surface $S$ in 3-space is parameterized by a function $p(s,t)=(x(s,t),y(s,t),z(s,t))$ defined on a rectangle $R=srange \times trange$, and $g$ is a function defined on $S$. So $g\circ p$ is defined on $R$ and might represent say the density of $S$ at $p(x,y)\in S$ for $(x,y)\in R$. Then the mass of $S$ would be $\iint_S g \, dA = \iint_R g(p(s,t)) ||p_s \times p_t|| \,ds\,dt$. In particular, if $g = 1$, then the integral would be the area of $S$. This interact (which was generated to my specification by CoCalc AI assistant!) computes the mass and center of mass. It also computes the average value of $g$ on the surface and attempts to plot points where the average value is attained.