A moving point $P(t)=[x(t),y(t),z(t)]$ in space as $t$ ranges over the interval $[a,b]$ traces out a path. The velocity $V=dP/dt$ is always tangent to the path and the normalized velocity or unit tangent is $T=V/(\|V\|)$ when $V$ is not the zero vector (ie when $V$ is not the zero vector).

The acceleration of $P$ is $dV/dt$, which is perpendicular to velocity when velocity is a constant nonzero vector. Hence $dT/dt$ is perpendicular to velocity. So when $N=(dT/dt)/\|dT/dt\|$ is a unit vector perpendicular to $T$ when $dT/dt$ is a nonzero vector. In that case, the binormal $B = T \times N$ is defined and we have a moving coordinate system ($TNB$ frame), shown in the diagram with $T$, $N$, $B$ red, green and black respectively.

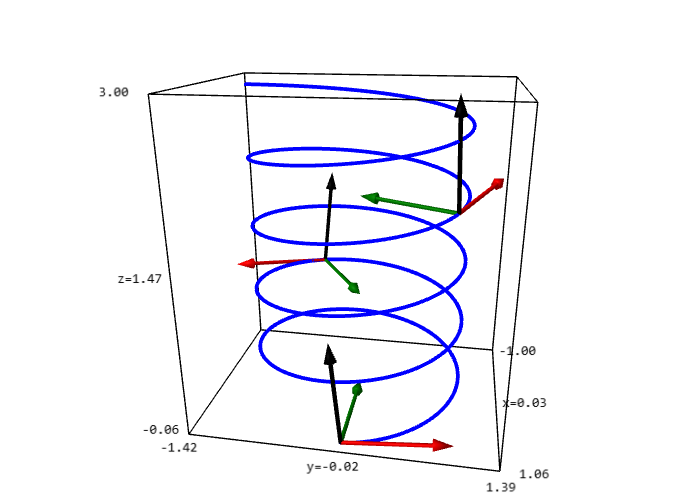
In the sagemath interact below, press start, then put in your path $[x(t),y(t),z(t)]$ and the parameters $[a,b,c,n,s]$ where $t$ (no other variable allowed) goes from $a$ to $b$, $c$ is the first $TNB$ frame beyond $a$, $n$ is the number of $TNB$ frames displayed equally spaced from $a+c$ to $b$, and $s$ is a scaling factor for the size of the frames (make it less than 1 if the frames are too large, greater than 1 if they're too small). Then press the update button.
Note: You can also plot paths in 2 dimensions such as $[cos(t),t\ sin(t)]$. Paths that are linear are not plotted since the normal $N$ is undefined.

Some parametric equations problems to solve.

1. Show that the path of the helix $[cos(t),sin(t),t/2 ]$ lies on a cylinder.

2. Write parametric equations for a point $P(t)$ that moves from $A=(1,1,0)$ to $B=(3,-3,2)$ along the straight line seqment connecting the points. Are these equations unique?

3. Write parametric equations for a point $P(t)$ that moves from the north pole $(0,0,5)$ of the sphere $x^2+y^2+z^2=25$ to the south pole, staying on the sphere as it moves.