Twitter problem

I like analytic geometry. You can discover new theorems by playing with the algebra. For example, by allowing the height to vary, we can discover that the above theorem generalizes to any rectangle:
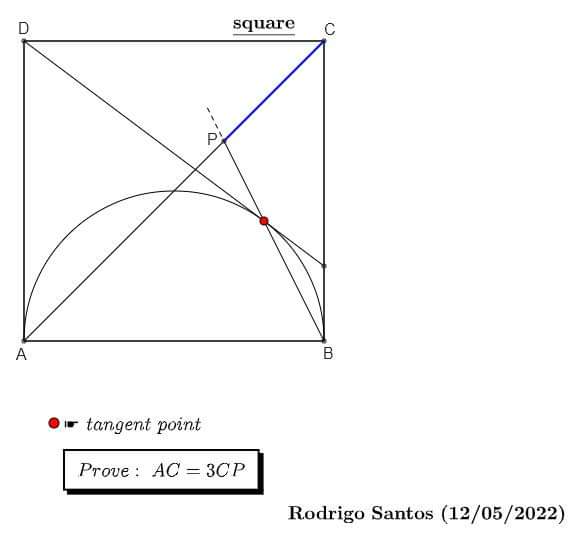
Draw a rectangle $[A,B,C,D]=[(0,0),(1,0),(1,b),(0,b)]$ with $b\gt 0$. Inscribe a semicircle on the base $AB$, and draw the tangent line from $D$ to the semicircle with negative slope, meeting the semicircle at $X=(t,s)$. Then draw the line through $B$ and $X$ to where it meets the diagonal $AC$ at $P=(x,b\cdot x)$. Show that $PC$ is 1/3 of $AC$ in all cases.
The theorem can be restated: On any rectangle, $ABCD$, mark the midpoint $M$ of segment $AB$, and mark the point $P$ on $AC$ where $CA/CP=3$. Now mark the point $X$ on $PB$ where $MX=BX$. Then the line $DX$ is tangent to the circle of radius $MB$ centered at $M$.
Problem. Find a synthetic proof of this. The analytic proof is straightforward, but doesn't provide insight.