Twitter problem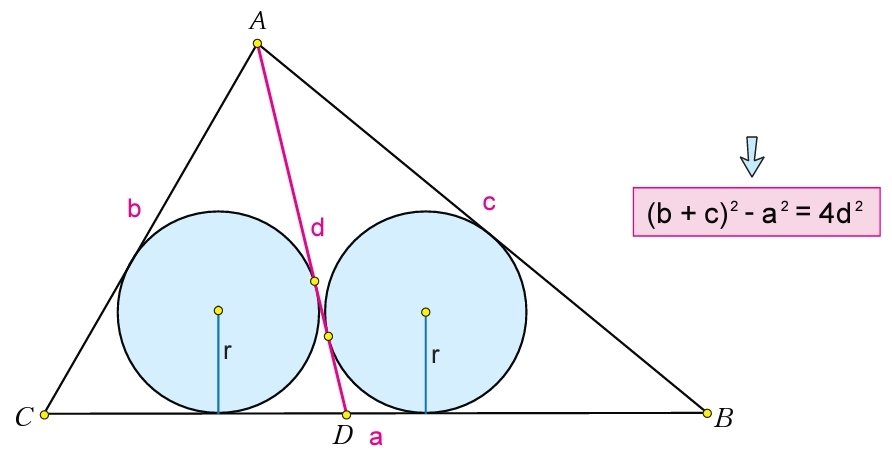

Here are some problems inspired by a problem from archimedes_000 on twitter.

Problem: Given a triangle $ABC$ with $A=(x,y)$, $B=(1,0)$, and $C=(0,0)$, find the point $D=(z,0)\in CB$ so that the incircles of $ACD$ and $ADB$ have the same radius.

Problem: A triangle has base 10 and base angles $\alpha$ and $\beta$ measured in degrees. Two tangent circles of radius r sit tangent to the base with each circle tangent to the side of the triangle nearest to it. Find the common radius.

Problem: Given $\triangle ABC$, let $D$ be the midpoint of $BC$, and $r_1$ and $r_2$ be the radii of the incircles of $\triangle ACD$ and $\triangle ADB$ respectively. Find $\displaystyle\frac{r_1}{r_2}$.