Interesting diagram posted by @Archimedes on twitter.
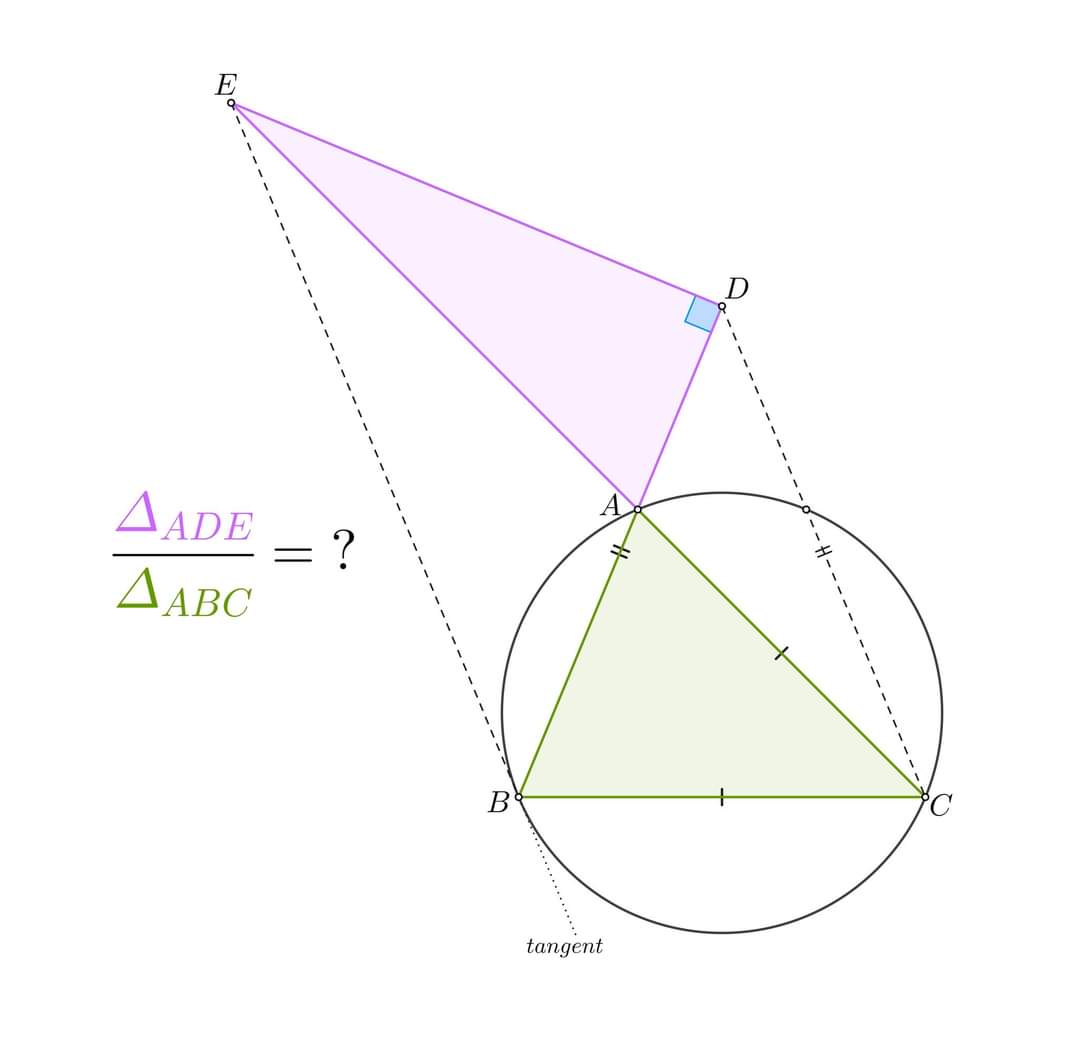 |
Looking at the figure, it appears that $BCDE$ is a trapezoid with $BE$ parallel with $CD$. If that were the case, the ratio $\text{area}ABC/\text{area}ADE$ is 1 since $\text{area}BCD=\text{area}CDE$ (they have the same height and same base), so $\text{area}ABC=\text{area}BCD-\text{area}ACD=\text{area}CDE-\text{area}ACD=\text{area}ADE$.
However, we are only given that $AC=BC$, $BD=CD$, and $\angle ADE = 90^o$, so we must show that this implies that $BE$ and $CD$ are parallel. Use analytic geometry to analyze this.
Set up a coordinate system with $A=(0,0)$, $B=(1,0)$, $C=(1/2,h)$, $D=(d,0)$ and $E=(d,y)$. Since $DB=DC$, $(a-d)^2 = (a/2-d)^2 + h^2$ so $d=3/4-h^2$. Since $E, A$ and $C$ are collinear, use slopes to obtain $y=2\,d\,h/a$. Equate the slopes of $BE$ and $CD$ to obtain a fifth degree polynomial in $h$, $p(h)=32\,h^5 - 48\,h^3 + 2\,h$, which factors to $p(h)=2\,(4\,h^2 + 4\,h - 1)\,(4\,h^2 - 4\,h - 1)\,h$, which has 5 real roots $0,\pm\frac{1}{2} \sqrt{3+2\,\sqrt{2}},\pm \frac{1}{2}\sqrt{3-2\,\sqrt{ 2}}$. Four of these are viable, yielding two diagrams, of which only the first satisfies all of the 3 given conditions.
|
Here's a variation on that problem, where we assume $AB=BC$,$AC=AD$, and $\angle ACE= 90^o$. You will notice a significant change in the solution.
|
|