Arcs of triangles in region 2 as described in the paper above, E is the equilateral triangle, I2 is the isosceles triangle with exactly two quadrisections, and I1 is the endpoint of the arc of triangles with exactly two quadrisections. You can expand these videos to screen size.

A Space of triangles

Every triangle is similar to exactly one triangle with vertices $(0,0),(1,0),(x,y)$ where $x \ge 1/2$, $y \gt 0$ and $x^2+y^2 \le 1$ (the blue area below referred to as Region 1 in the paper above). You can investigate quadrisections of triangles below by choosing coordinates $(x,y)$ satisfying these conditions. Alternatively, set the mode to 1 and choose coordinates $(t1,t2)$ satisfying $0\lt t1 ,t2 \le 1$. As shown in the above paper, all triangles have exactly one quadrisection except for the ones near E, the equilateral triangle. They all have three quadrisections, except for a short arc of triangles with two quadrisections stretching from I1 to I2.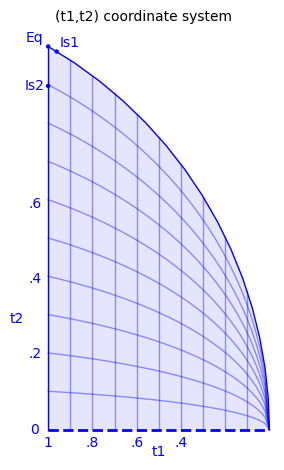