Quadrisections of convex polygons.
This page has several different sage interacts designed to investigate the quadrisections of convex polygons. See this paper (draft).
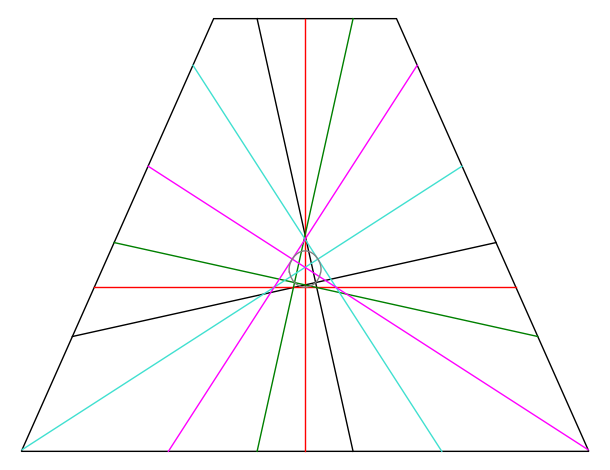
This page has several different sage interacts designed to investigate the quadrisections of convex polygons. See this paper (draft).
Given an arbitrary convext polygon P a secant $XY$ (a segment with endpoints $X$, $Y$ on the boundary of P ) is called a bisector if it divides P into 2 equal areas. Note each secant of P is parallel to exactly one bisector of P. An orthogonal pair of bisectors of P is said to quadrisect P if they divide P into 4 equal areas. In this page, we use an algorithm (developed using elementary vector algebra in the paper above) for finding all the quadrisections of an arbitrary convex polygon.
In order to begin, you first must click the top button to load the procedures needed. If things get messed up, you can always begin over by refreshing your browser and clicking the top button again.
An interact to find the quadrisections of a convex polygon with a given set of vertices.Put in the vertices of a convex polygon in counterclockwise order and press Start to see its quadrisections, and the corresponding area function showing the % deviation from a quadrisection. This function crosses the x-axis at each quadrisection. |
An interact to experiment with the area function of orthogonal parallelograms.Each convex polygon with n sides is covered by a set of n or less pairs of orthogonal parallelograms whose diagonals are bisectors of the polygon, and so the area function for the polygon is piecewise defined by the area functions of the parallelograms. (See above paper.) AC1 and AC2 are the endpoints of the major diagonal, alpbet1 and alpbet2 are the angles of the sides of the respective parallelograms, and thet is the angle between the major and minor diagonals of both parallelograms. win designates the size of the window about the track of the intersection of the orthogonal diagonals. |