A model for the space of quadrilaterals

Carl Eberhart, [email protected]

This page has several different sage interacts designed to investigate a model for the space of convex quadrilaterals, as defined in this paper. or this revision.

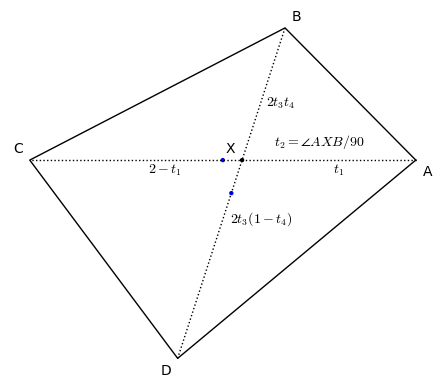
A quadrilateral $ABCD$ is in the model if
$A=(1,0)$, $C=(-1,0)$, $X=(t_1,0)$, $B=X+2t_3t_4\,(\cos(t_2\,\pi/2),\sin(t_2\,\pi/2))$, $D=X-2t_3(1-t_4)\,(\cos(t_2\,\pi/2),\sin(t_2\,\pi/2))$,
where the parameters are defined by $t_1=AX$, $t_2$ is the ratio of the measure of $\angle AXB$ in degrees to 90 degrees, $t_3=BD/2$, and $t_4=BX/BD$, and satisfy the constraints below. Note: In the revised paper, we rescale $t_2$ to remove the dependence on the transcendental sine and cosine functions.
$$t_1,t_2,t_3 \in (0,1], \text{ and } t_4 \in (0,1) , \text{ with } t_4 \in (0,1/2]\text{ when } t_1=1 \text{ or } t_2=1, \text{ and } t_4 \in (0,t_1/2] \cup [1-t_1/2,1) \text{ when } t_3=1$$
In each interact, you can set the parameters $t_1, t_2, t_3, t_4$ to desired values and press the Update button to display the corresponding polygon. Note that the polygon is black if it is in the model, otherwise it is red. To see the quadrilateral's classification, check the box for that. To see the quadrisections, check the box for that.

In order to begin, you first must click the top button to load the procedures needed. If things get messed up, you can always begin over by refreshing your browser and clicking the top button again.

To Begin, click this button first.

An interact to find the placement of any quadrilateral in the model.

Put in the vertices of a quadrilateral (or a set of 4 parameters in (0,1]) and press Start to see its representative in the space of quadrilaterals. Note there are 1, 2, 4 or 8 placements of which only one, the black one, is in the model $\mathbb{Q}$. The parameters for each placement are shown on the placement.

A sagelet to investigate quadrisections of convex quadrilaterals

Use one of 2 different methods of specifying the quadrilateral.
If method = t, then use the standard model parameters [$t_1, t_2, t_3, t_4$].
If method = ABCD, then enter the vertices of the quadrilateral in counterclockwise order [A,B,C,D].

Experiment with the parameters $t_1,t_2,t_3,t_4$ in T, parameters $\angle BXA$, and lengths MX, XB, XD in R, or parameters B=(x,y), D=(z,w) in xyzw.

Here you can experiment with the t parameters by sliding the values and pressing Update. Note that when all values are in $(0,1)$, the quadrilateral is black.

In this interact, put in values $[t_1,t_2,t_3,t_4]$ for the parameters to see what quadrilateral you get. You can also classify it, and get its quadrisections.

Cyclic, Tangential, or Extangential Quadrilaterals

A quadrilateral is cyclic if its vertices lie on a circle, tangential if there is a circle tangent to each of its sides, and extangential if there is a circle which is tangent to each of its extended sides.

Cyclic Quadrilaterals are characterized by $t_1=1-\sqrt{1-4 t_3^2 t_4 (1-t_4)}$. Here is a sagelet to play with the parameters.

Tangential and extangential quadrilaterals are best described by specifying 3 angles: $\alpha,\beta,\gamma$.If $\alpha+\beta+\gamma \gt 180$ then we get a tangential quadrilateral and if $\alpha+\beta+\gamma \lt 180$, we get an extangential quadrilateral. If the quadrilateral is red, it is not in the model.

Circumscribing Ellipses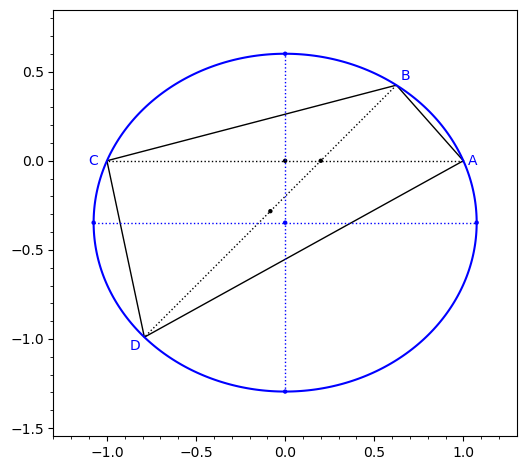

It turns out that every quadrilateral has lots of circumscribing ellipses. In particular,

Each quadrilateral has a circumscribing ellipse one of whose axes is parallel with a major diagonal.
To see this let $ABCD$ be a quadrilateral labelled counterclockwise so that $AC$ is a major diagonal. Set up a coordinate system with $A=(1,0)$, $B=(x_1,y_1)$, $C=(-1,0)$, $D=(z_1,w_1)$. The equation for an ellipse with an axis parallel to $AC$ can be written $\displaystyle\frac{x^2}{a^2}+\frac{(y-k)^2}{b^2}=1$. Plug the vertices into the equation and solve for $a,b,k$ to get $$k=\frac{2(w_1 x_1^2 - y_1z_1^2 - w_1 + y_1)}{w_1^2x_1^2 - y_1^2z_1^2 - w_1^2 + y_1^2}$$ $$a=\frac{ 4(w_1x_1^2 - y_1z_1^2 - w_1 + y_1)(w_1 - y_1)w_1y_1}{(w_1x_1 + y_1z_1 + w_1 - y_1)(w_1x_1 + y_1z_1 - w_1 + y_1)(w_1x_1 - y_1z_1 + w_1 - y_1)(w_1x_1 - y_1z_1 - w_1 + y_1)}$$ $$b=\frac{ 4(w_1x_1^2 - y_1z_1^2 - w_1 + y_1)^2}{(w_1x_1 + y_1z_1 + w_1 - y_1)(w_1x_1 + y_1z_1 - w_1 + y_1)(w_1x_1 - y_1z_1 + w_1 - y_1)(w_1x_1 - y_1z_1 - w_1 + y_1))}$$ Then substitute these values back into the equation and simplify to get $$(w_1^2y_1 - w_1y_1^2)x^2 + (w_1x_1^2 - y_1z_1^2 - w_1 + y_1)y^2 - (w_1^2x_1^2 - y_1^2z_1^2 - w_1^2 + y_1^2)y - w_1^2y_1 + w_1y_1^2=0 $$ Here's a sagelet to see this for quadrilaterals in the model.

Simple nonconvex quadrilaterals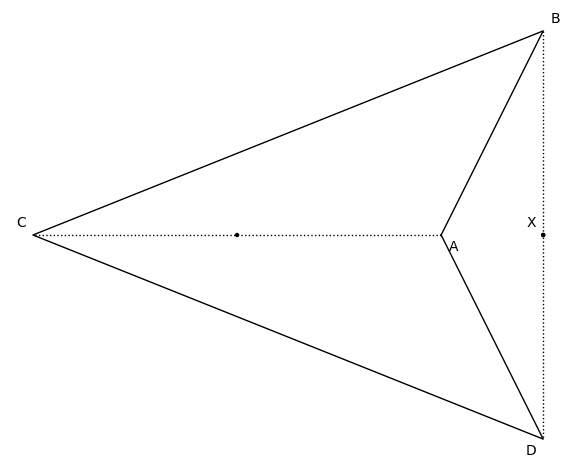

Here you can explore the simple non convex quadrilaterals (the sides form a simple closed curve but the interior is not convex) with the parameters by sliding the values and pressing Update. These occur when $t_1$ is negative. They also occur when $t_1$ is positive and $t_4$ is negative, however those are duplicates.