This page has several different sage interacts designed to investigate the parameter space $\mathbb{P}$ for the model $\mathbb{Q}$ of the space of convex quadrilaterals, as defined in this paper, or this revision.

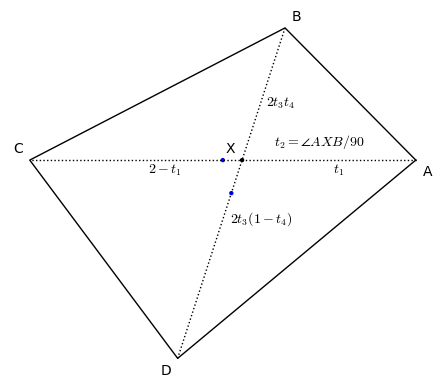
A quadrilateral $ABCD$ is in the model if
| $t_1,t_2,t_3 \in (0,1]$ and $t_4 \in (0,1)$, | $t_4 \in (0,1/2]$ when $t_1=1$ or $t_2=1$, | and $t_4 \in (0,t_1/2]\cup [1-t_1/2,1)$ when $t_3=1$ |
Thus, each quadrilateral corresponds to a unique point $(t_1,t_2,t_3,t_4) \in \mathbb{P}$, and you use the parameter space to visualize the relations between various classes of quadrilaterals.
In order to begin, you first must click the top button to load the procedures needed. If things get messed up, you can always begin over by refreshing your browser and clicking the top button again.
|
|
| tall trapezoids: yellow | short trapezoids: pink |
| cyclic quadrilaterals: turquoise | tangential quadrilaterals: magenta |
| extangential 1 quadrilaterals: green | extangential 2 quadrilaterals: orange |
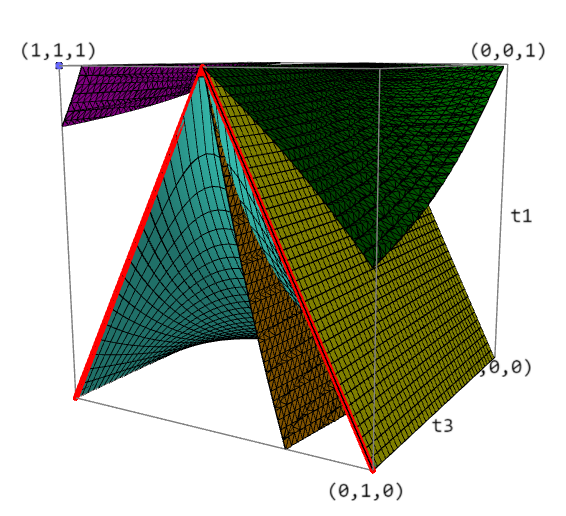
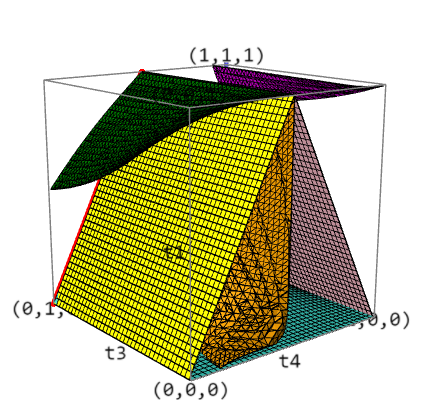
This sagelet is very useful to see the relation between various classes of quadrilaterals. Note the cross-section of the trapezoids and also the cross-section of the cyclic quadrilaterals remains unchanged as $t_2$ varies. This tells us that their graphs are the cross-section crossed with $(0,1]$. By checking two classes at once, you may see a one dimensional cross-section of the two dimensional class defined by their intersection. By playing with this sagelet, you can convince yourself that (1) the trapezoid graph separates the parameter space into 3 pieces, (2) the cyclic graph separates the middle quadrilaterals into 2 pieces and intersects the trapezoids in the equilateral trapezoids.
In this sagelet, select values $0 \lt t_1, t_2, t_3 \le 1, 0 \lt t_4\le 1$ for a quadrilateral $\mathcal{Q}$ and see how many copies of it lie in $\mathbb{P}$. If $t_1, t_2, t_3 \lt 1$, then $\mathcal{Q}$ lies in the interior of $\mathbb{P} $ and there is only one copy. If at least one of $t_1, t_2, t_3$ is $1$, there are 1, 2 or 3 additional copies of $\mathcal{Q}$ in $\overline{\mathbb{P}}$, and only one of them is in $\mathbb{P}$. It is the grey dot in the model and is shown below in black. The others are red dots in the model and shown below in red. For example, try $t_1=1, t_2=.8, t_3=1, t_4=.7$.
The $t_1=1$ and $t_2=1$ boundaries of $\mathbb{P}$ are easy to see. For example, if $t_1=1$, then except when $t_4=.5$, $(1,t_2,t_3,t_4)$ and $(1,t_2,t_3,1-t_4)$ are (distinct) congruent members of $\overline{\mathbb{P}}$ under 180 degree rotation about $(0,0)$, so we choose the member for which $t_4\le .5$ to be in $\mathbb{P}$. So the $t_1=1$ boundary is 'bottom half' of the $t_1=1$ face of $\mathbb{I}^4$. Similarly, the $t_2=1$ boundary of $\overline{\mathbb{P}}$ is the bottom half of the $t_2=1$ face of $\mathbb{I}^4$. The $t_3=1$ boundary of $\mathbb{P}$ is the most interesting. It is still one of the $t_3=1$ face of $\mathbb{I}^4$, but it could be described as 'a' bottom quarter together with 'a' top quarter of the $t_3=1$ face of $\mathbb{I}^4$. In this sagelet, you can put in the $t_1$, $t_2$, and $t_4$ parameters for a quadrilateral with $t_3=1$ and see where it lies in the $t_3=1$ boundary of $\mathbb{P}$. It is shown as the black point, and the congruent members of $\overline{\mathbb{P}}$ not in $\mathbb{P}$ are shown as the red point(s). Note when $t_2=1$, $t_1 \lt 1$, and $t_4 \ne .5$, there are 3 red points.
In this sagelet, you can put in the $\alpha,\beta,\gamma$ parameters for a tangential or extangential quadrilateral and see where it lies in the particular $t_2$ cross section of the parameter space. Keep $\gamma \ge \beta$ so as to keep the slope of $BD$ positive or $\infty$. The type of quadrilateral you get depends on $\delta=\alpha+\beta+\gamma$. If $\delta > 180$, you get a tangential quadrilateral. If $\delta \lt 180$, you get an extangential quadrilateral, with the cutpoint between extangential A and B occuring near $\delta = 112$ degrees. Interesting problem: determine the cutpoint exactly. It is not constant. It is a function of $\alpha, \beta, \gamma$. If it lies outside the model, the quadrilateral is red.
In this sagelet, you can put in the $\alpha,\beta,\gamma$ parameters for a tangential or extangential quadrilateral and see where it lies in the particular $t_2$ cross section of the parameter space. Keep $\gamma \ge \beta$ so as to keep the slope of $BD$ positive or $\infty$. The type of quadrilateral you get depends on $\delta=\alpha+\beta+\gamma$. If $\delta > 180$, you get a tangential quadrilateral. If $\delta \lt 180$, you get an extangential quadrilateral, with the cutpoint between extangential A and B occuring near $\delta = 112$ degrees. Interesting problem: determine the cutpoint exactly. It is not constant. It is a function of $\alpha, \beta, \gamma$. If it lies outside the model, the quadrilateral is red.
In this sagelet, you can put in the $\alpha,\beta,\gamma$ parameters for a tangential or extangential quadrilateral and see where it lies in the particular $t_2$ cross section of the parameter space. Keep $\gamma \ge \beta$ so as to keep the slope of $BD$ positive or $\infty$. The type of quadrilateral you get depends on $\delta=\alpha+\beta+\gamma$. If $\delta > 180$, you get a tangential quadrilateral. If $\delta \lt 180$, you get an extangential quadrilateral, with the cutpoint between extangential A and B occuring near $\delta = 112$ degrees. Interesting problem: determine the cutpoint exactly. It is not constant. It is a function of $\alpha, \beta, \gamma$. If it lies outside the model, the quadrilateral is red.